什么是三角函数
三角函数是以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。下面学习啦小编就给大家介绍三角函数的相关信息。
三角函数的定义
直角三角形三角函数定义
在直角三角形中,当平面上的三点A、B、C的连线,AB、AC、BC,构成一个 直角三角形,其中∠ACB为 直角。对∠BAC而言, 对边(opposite)a=BC、 斜边(hypotenuse)c=AB、邻边(adjacent)b=AC,则存在以下关系:
基本函数 | 英文 | 缩写 | 表达式 | 语言描述 | |
正弦函数 | sine | sin | a/c | ∠A的对边比斜边 | |
余弦函数 | cosine | cos | b/c | ∠A的邻边比斜边 | |
正切函数 | tangent | tan | a/b | ∠A的对边比邻边 | |
余切函数 | cotangent | cot | b/a | ∠A的邻边比对边 | |
正割函数 | secant | sec | c/b | ∠A的斜边比邻边 | |
余割函数 | cosecant | csc | c/a | ∠A的斜边比对边 |
注:正切函数、余切函数曾被写作 、 现已不用这种写法
变化规律
正弦值在
随角度增大(减小)而增大(减小),在
随角度增大(减小)而减小(增大); 余弦值在
随角度增大(减小)而增大(减小),在
随角度增大(减小)而减小(增大); 正切值在
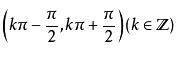
随角度增大(减小)而增大(减小); 余切值在
随角度增大(减小)而减小(增大); 正割值在
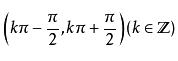
随着角度的增大(或减小)而增大(或减小); 余割值在
随着角度的增大(或减小)而减小(或增大)。
注:以上其他情况可类推,参考第五项:几何性质。
除了上述六个常见的函数,还有一些不常见的三角函数:

任意角三角函数定义:
在 平面直角坐标系xOy中设∠β的始边为x轴的正半轴,设点P(x,y)为∠β的终边上不与原点O重合的任意一点,设r=OP,令∠β=∠α,则:
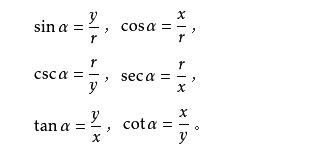
单位圆定义
六个三角函数也可以依据 半径为1中心为原点的 单位圆来定义。单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于 直角三角形。但是 单位圆定义的确允许三角函数对所有 正数和 负数辐角都有定义,而不只是对于在 和 弧度之间的角。它也提供了一个图像,把所有重要的三角函数都 包含了。根据 勾股定理, 单位圆的 方程是:对于圆上的任意点 。
图像中给出了用 弧度度量的一些常见的角:逆时针方向的度量是 正角,而顺时针的度量是 负角。设一个过 原点的线,同 轴正半部分得到一个角 ,并与单位圆相交。这个交点的 和 坐标分别等于 和 。图像中的三角形确保了这个公式;半径等于斜边且长度为1,所以有 和 。单位圆可以被视为是通过改变邻边和对边的长度,但保持斜边等于 1的一种查看无限个三角形的方式。
对于大于 或小于等于 的角度,可直接继续绕单位圆旋转。在这种方式下,正弦和余弦变成了周期为 的 周期函数:对于任何角度 和任何 整数 。
周期函数的 最小正周期叫做这个函数的“ 基本周期”。正弦、余弦、正割或余割的基本周期是全圆,也就是 2π弧度或 360°;正切或余切的基本周期是半圆,也就是 π 弧度或 180°。上面只有正弦和余弦是直接使用单位圆定义的,其他四个三角函数的定义如图所示。
在 正切函数的图像中,在角 π 附近变化缓慢,而在接近角 ( + 1/2)π 的时候变化迅速。正切函数的图像在 θ = ( + 1/2)π 有垂直渐近线。这是因为在 θ 从左侧接进 ( + 1/2)π 的时候函数接近 正无穷,而从右侧接近 ( + 1/2)π 的时候函数接近负无穷。
另一方面,所有基本三角函数都可依据中心为 的单位圆来定义,类似于历史上使用的几何定义。特别 是,对于这个圆的 弦 ,这里的 θ 是对向角的一半,sin 是 (半弦),这是印度的 阿耶波多介入的定义。cos 是水平距离 ,versin =1-cos 是 。tan 是通过 的 切线的 线段 的长度,所以这个函数才叫 正切。cot 是另一个切线段 。 sec = 和 csc = 是割线(与圆相交于两点)的线段,所以可以看作 沿着 A 的切线分别向水平和垂直轴的投影。 是 exsec = sec -1(正割在圆外的部分)。通过这些构造,容易看出 正割和正切函数在 θ 接近 π/2的时候发散,而余割和余切在 θ 接近零的时候发散。
依据单位圆定义,我们可以做三个 有向线段( 向量)来表示正弦、余弦、正切的值。如图所示,圆O是一个单位圆,P是 的 终边与单位圆上的交点,M点是 在 轴的投影, (1,0)是圆O与x轴 正半轴的交点,过A点做过圆O的 切线。
那么向量 MP对应的就是 的 正弦值,向量 OM对应的就是余弦值。OP的 延长线(或 反向延长线)与 的切线的交点为T,则向量A T对应的就是 正切值。向量的起止点 不能颠倒,因为其方向是有意义的。
借助线三角函数线,我们可以观察到 第二象限角α的正弦值为正, 余弦值为负, 正切值为负。
级数定义
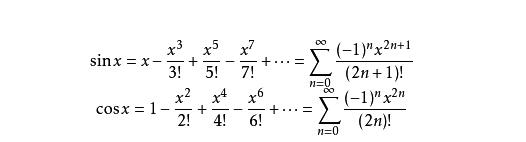
只使用几何和 极限的性质,可以证明正弦的 导数是余弦,余弦的导数是负的正弦。(在 微积分中,所有角度都以 弧度来度量)。我们可以接着使用 泰勒级数的理论来证明下列 恒等式对于所有 实数 都成立:
这些恒等式经常被用做正弦和余弦函数的定义。它们经常被用做三角函数的严格处理和应用的起点(比如,在傅里叶级数中),因为 无穷级数的理论可从 实数系的基础上发展而来,不需要任何几何方面的考虑。这样,这些函数的可微性和 连续性便可以单独从级数定义来确立。
其他级数可见于:
注:Un是n次上/下数, Bn是n次伯努利数,∣x∣<π/2。
三角函数的诱导公式
公式内容
| 公式一
| 公式二 |
sin(2kπ+α)=sin α cos(2kπ+α)=cos α tan(2kπ+α)=tan α cot(2kπ+α)=cot α sec(2kπ+α)=sec α csc(2kπ+α)=csc α | sin(π+α)=-sin α cos(π+α)=-cos α tan(π+α)=tan α cot(π+α)=cot α sec(π+α)=-sec α csc(π+α)=-csc α |
| 公式三 | 公式四 |
sin(-α)=-sin α cos(-α)=cos α tan(-α)=-tan α cot(-α)=-cot α sec(-α)=sec α csc(-α)=-csc α | sin(π-α)=sin α cos(π-α)=-cos α tan(π-α)=-tan α cot(π-α)=-cot α sec(π-α)=-sec α csc(π-α)=csc α |
| 公式五 | 公式六
|
sin(α-π)=-sin α cos(α-π)=-cos α tan(α-π)=tan α cot(α-π)=cot α sec(α-π)=-sec α csc(α-π)=-csc α | sin(2π-α)=-sin α cos(2π-α)=cos α tan(2π-α)=-tan α cot(2π-α)=-cot α sec(2π-α)=sec α csc(2π-α)=-csc α |
| 公式七 | 公式八 |
sin(π/2+α)=cosα cos(π/2+α)=−sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sec(π/2+α)=-cscα csc(π/2+α)=secα | sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sec(π/2-α)=cscα csc(π/2-α)=secα |
| 公式九 | 公式十 |
sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sec(3π/2+α)=cscα csc(3π/2+α)=-secα | sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα sec(3π/2-α)=-cscα csc(3π/2-α)=-secα |
推导方法
定名法则
90°的奇数倍+α的三角函数,其绝对值与α三角函数的绝对值互为 余函数。90°的 偶数倍+α的三角函数与α的三角函数绝对值相同。也就是“奇余偶同,奇变偶不变”。
定号法则
将α 看做锐角(注意是“看做”),按所得的角的象限,取三角函数的符号。也就是“象限定号,符号看象限”(或为“ 奇变偶不变,符号看象限”)。
在Kπ/2中如果K为偶数时函数名不变,若为奇数时函数名变为相反的函数名。 正负号看原函数中α所在 象限的正负号。关于 正负号有个口诀;一全正,二正弦,三两切,四余弦,即第一象限全部为正,第二象限角,正弦为正,第三象限,正切和余切为正,第四象限,余弦为正。或简写为“ASTC”,即“all”“sin”“tan+cot”“cos”依次为正。还可简记为:sin上cos右tan/cot对角,即sin的正值都在x轴上方,cos的正值都在y轴右方,tan/cot 的正值斜着。
比如:90°+α。定名:90°是90°的 奇数倍,所以应取余函数;定号:将α看做锐角,那么90°+α是第二象限角,第二象限角的正弦为正,余弦为负。所以sin(90°+α)=cosα , cos(90°+α)=-sinα 这个非常神奇,屡试不爽~
还有一个口诀“ 纵变横不变,符号看象限”,例如:sin(90°+α),90°的终边在纵轴上,所以函数名变为相反的函数名,即cos,所以sin(90°+α)=cosα。
猜你感兴趣:
2.数学与三角函数
3.三角函数学习方法



